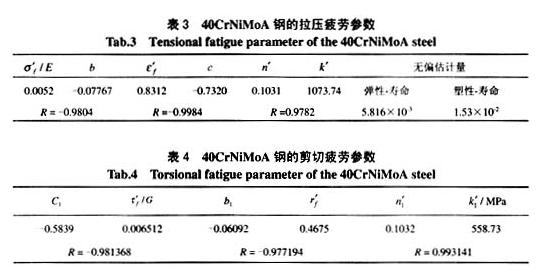
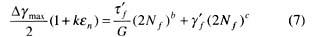參考文獻[1～3]，經過相關性檢驗，常溫下應變-壽命關系均按照Manson-Coffin公式擬合，在實驗中，選用了95%的置信度，5%的誤差限，擬合數據及循環應力應變特性參數見表3、表4所示（R為相關系數）。
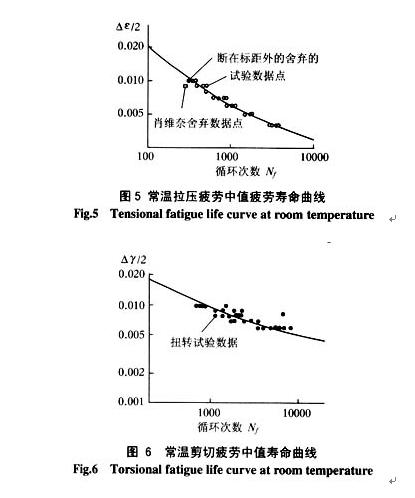
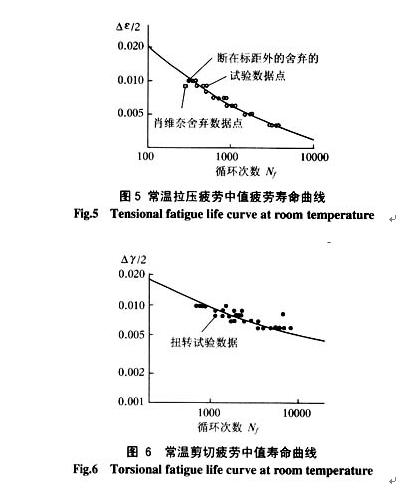
兩種加載方式下經最小二乘法擬合的中值疲勞壽命曲線分別如圖5、圖6所示。圖5中，小實黑點表示由于斷口位于標距外而被排除的試驗數據；方框點是根據“肖維奈準則”而得到的舍棄點。斷在標距外的原因可能是應力集中及加工原因。圖6中的小實黑點表示試驗數據點，穿過試驗點的曲線是擬合的剪切疲勞壽命曲線。由圖可知，擬合的疲勞壽命曲線與試驗數據吻合較好。
4 多軸壽命模型的評估
4.1 Von Mises等效應變范圍模型[1]
由于多軸疲勞實驗本身的復雜性以及實驗費用之高，因而很有必要尋找一種“橋梁”能通過簡單的、相對廉價的單軸疲勞實驗預測多軸疲勞壽命，下面將利用這些現有模型使拉壓疲勞與剪切疲勞聯系起來以達到簡化實驗的目的。
該方法采用了塑性理論中的Von Mises等效應變范圍法。對純扭轉，泊松比v可假定為0.5（假定塑性應變為主，體積不變），等效應力應變的公式如下：
式中 △εeq為等效應變范圍； Nf為循環次數。
用該模型預測的扭轉疲勞壽命如圖7所示。圖中的小圓點表示經過對同一應變水平求平均而得的扭轉疲勞壽命試驗點。
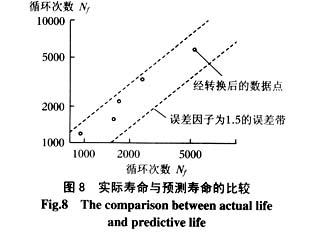
由圖7可知，該模型在大應變時高估扭轉疲勞壽命，而在小應變時低估了疲勞壽命。圖8為模型的壽命預測值與實際壽命的比較。由圖8可見：用von Mises等效應變模型可以很好預測扭轉疲勞壽命，誤差因子在1.5以內。
4.2 Manson-Halford模型[1]
Manson 和 Halford（1977）提出了基于應力的多軸應力因子（MF）修正的Von Mises等效應變范圍模型。這種多軸應力因子(MF)又是基于Davis和Connelly(1959)所提出的三維因子(TF)。將用MF修正過的等效塑性應變范圍代入軸向塑性應變壽命方程，可以估計出扭轉疲勞壽命。Manson-Halford模型考慮了材料韌性隨著應力狀態變化的特性。材料在常溫時的應變壽命關系如下所示
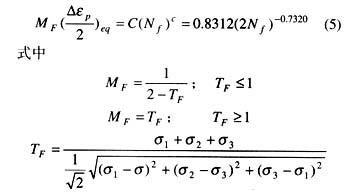
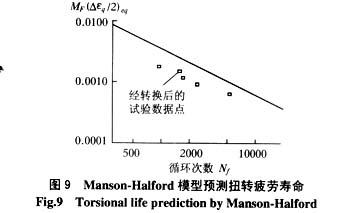
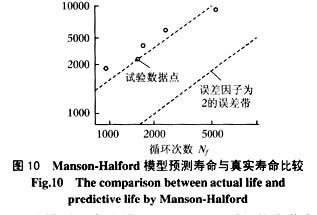
圖9中，圖中數據點為同一應變水平求平均后的扭轉疲勞壽命點。如圖所示該模型高估了真實的扭轉疲勞壽命而顯得過分冒險。圖10為用該模型預測的扭轉疲勞壽命與實際扭轉疲勞壽命的比較。
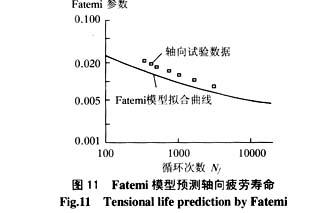
4.3 Fatemi 模型[1]
該模型采用以剪切常數為基礎來預測疲勞壽命，模型的表達式為：
為最大工程剪應變范圍。
此模型對實驗數據進行擬合，所得的疲勞壽命曲線如圖11所示。圖中的小方框代表同一應變水平求均值后的軸向疲勞壽命試驗數據點。
由圖11可知，該模型預測軸向拉壓疲勞壽命時會低估疲勞壽命，將預測的疲勞壽命與真實壽命作一比較如圖12所示。可以認為：Fatemi模型預測壽命低于真實壽命，趨于保守，誤差因子在2以外。
4.4 基于剪切形式的預測模型[5，6]
與前一模型一樣，此模型也以剪切常數為基礎來建立壽命估算模型，建立剪切形式的Manson-Coffin方程。該模型認為，損傷參量應是剪切應變與法向應變相結合的形式，提出用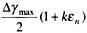
作為多軸加載條件下的等效多軸損傷參量。公式如下：
